Dielectric electroholographic gratings are electrically controlled Bragg gratings implemented by periodic striations that were produced during the crystal growth. The striations gratings are periodic modulation in the composition. In electrooptic paraelectric crystals these induce a periodic spatial modulation in the static (low frequency) dielectric constant, which upon the application of an external field induce a refractive index grating through the (quadratic) electrooptic effect.
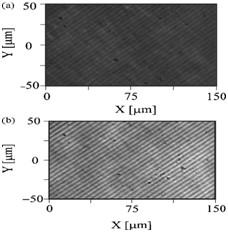
Figure 1: Images of a striation grating with a period of Λ = 4.21 μm scanned by an input beam polarized at 45° to the grating vector, and the output polarizer aligned to maximize the contrast. (a) When the applied electric field is zero. (b) Under an electric field E = 1.53 kV / cm.
It is well established that the phase transition temperature TC of ferroelectric oxygen perovskites is strongly affected by the presence of impurities and defects. For example, the replacement of a Ta ions in potassium tantalate niobate (KTN) by x % per mole of Nb ions will cause a change in TC given by Tc [K] ≈682x+33.2 [REF1]. A similar effect can be achieved by replacing a K ion in KTN by Li. Here the effect is more dramatic and results in certain cases in : δTC≈50 K° /1% per mole of Li [KLTN]. Thus, at the paraelectric state where the dielectric constant is given by the Curie law, a spatial variation in the composition that causes a correlated modulation in the Curie temperature (designated by : δTC (x)) will yield a change in the dielectric constant given by:
![]()
(1)
where ε is the relative static (and low frequency) dielectric constant, C is the Curie-Weiss constant, and T is the temperature. Applying a uniform electric field E to a crystal in which δTC is modulated will generate a modulation in the induced polarization P that is spatially correlated with δε(x) and is given by:
![]() (2)
(2)
where it is assumed that the crystal is slightly above TC so that εr>>1. At the paraelectric phase where the electrooptic effect is quadratic, the electric field induced birefringence is given by:
![]() (3)
(3)
where no is the index of refraction at the paraelectric phase, and geff is the effective quadratic electrooptic coefficient. Note that for a KTN crystal at T=Tc+7K where εr=104, geff=0.2m²/C² , and an applied field of E = 3 kV/cm, equation (3) yields induced birefringence of Δn≈0.01!
Finally, combining (1), (2) and (3) will yield the spatially modulated induced birefringence:
![]() (4)
(4)
Dielectric EH gratings are described in detail in [REF16].

