Since 1981 Israel’s National Insurance Institute (NII) has paid non-means-tested benefit to parents of children up to 18 years diagnosed with ASD. In December 2013 this benefit was 2,439 shekels a month, or about 27% of average wages. Diagnosis is undertaken independently of NII by relevant health professionals according to DSM criteria. The parents of children diagnosed with ASD may apply to NII for benefit. On confirmation, benefit payments are back-dated to the date of diagnosis. Details of diagnosis criteria, the application process, and the granting of eligibility for benefit may be found in Raz et al (2014). In addition, parents of eligible children benefit from higher income tax thresholds, reduced rates paid to local authorities, and their children have access to special education and therapies. Because the economic incentive to receive these and related benefits is large, probably most (if not all) children diagnosed with ASD in Israel feature in NII’s administrative records (Raz et al 2014).

Beneficiaries aged 16 in 1981 would be 50 years old today. Unfortunately, these early data were not preserved. The earliest record in our data refer to children born in 1984, aged about 30 in 2013.  We identify all children who were eligible for benefits on the grounds of ASD in any month during January 2003 to August 2014. Of these, we selected all individuals who were at least 18 years old in December 2013.

Although the data distinguish between economic branches according to standard ILO (International Labor Office) definitions, they do not distinguish between occupations and employers. Hence, it is difficult to analyse labor market mobility unless employees happened to move between economic branches. Here we present data on the distribution of employment between economic branches as well as data on mobility between economic branches. These data testify to a high degree of mobility between economic branches. They also show that members of the study group worked in all branches of the economy. These data understate true mobility because study group members who switched employers in the same economic branch go unrecorded. 

The economic branches in which the employed worked, which are many and varied. Figure SM1 shows the economic branches in which the study group worked during 2003 - 2012. In 2012 the largest economic branches were accommodation, food services and entertainment, and other services. The importance of these branches varied over time. More generally, study group members were represented in all major economic branches.

Figure SM1 Distribution of Employment by Economic Branch

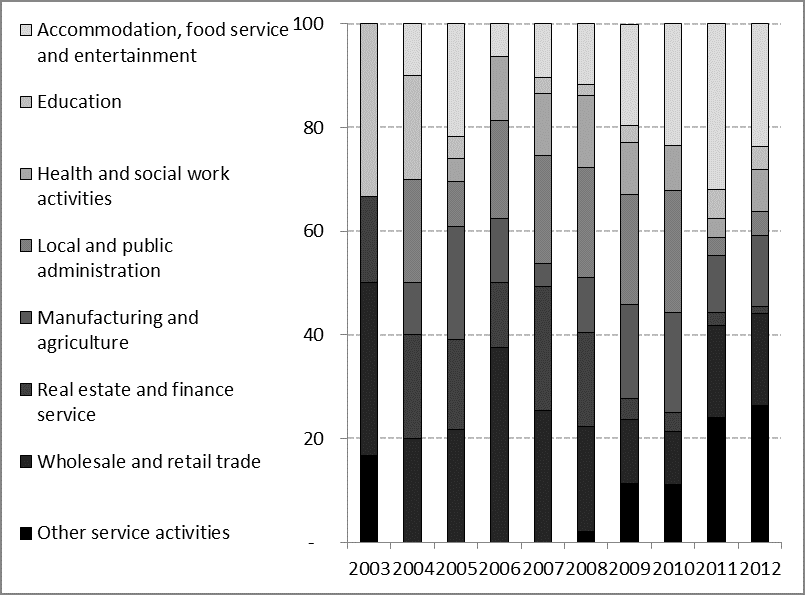
Bars show the sectoral distribution of employment for study group members by year.

Just as earnings are upwardly mobile, so is there a high degree of mobility in the economic branches chosen by the study group. Table SM1 shows that out of the 99 members of the study group who were employed two years, almost a half worked in two different economic branches. Out of the 71 members employed three years, 60.6% worked in two different economic branches and almost 20% worked in three economic branches. Table SM1 understates the degree of mobility in employment because, the data do not refer to work establishments. For example, workers who switched employer within the same economic branch are not counted in Table SM1. Nor are workers employed in more than one economic branch within calendar years. In summary, Figure SM1 and Table SM1 point to a high degree of labor market mobility among members of the study group. 

Table SM1 Employment Mobility between Economic Branches

(percent)

The table reports the number of economic branches in which study group members worked by the number of years that they were employed.

The incidentally truncated regression method (ITR Heckman 1976) hypothesizes two populations. The first population does not participate in the outcome of interest hence the outcome is zero, and the second participates in which event the outcome is positive. Let y_i denote the outcome for individual i, which is zero if she belongs to the first population, and is positive if she belongs to the second. Positive outcomes are hypothesized to depend on a set of covariates X_i with regression residual denoted by u_i. A latent variable y_i* is hypothesized to depend on covariates Z_i and a random variable e_i, which measures individual i’s unobserved susceptibility to participate. If y_i* is insufficiently small (negative) individual i belongs to the first population in which case y_i is negative, and is positive otherwise.

ITR assumes that u and e are bivariate normal random variables with correlation denoted by r, which is a parameter to be estimated. If r is positive, individuals with a greater susceptibility to participate (e) have larger positive outcomes for y if they participate. For example, individuals with a greater susceptibility to employment, work more if they are employed.  If r is negative, individuals more susceptible to participate have smaller outcomes if they participate. If r is zero, the two populations are independent, in which case it would have been appropriate to estimate the relation between y and X using data for the second population on its own.

The probability of participation for individual i equals F_i = F(z_i) where z_i = a + βZ_i has a standard normal distribution. Let P denote the rate of participation in the data, and z* = F^-1(P) denote the value of z, which is implied by the average rate of participation in the data.  The marginal effect of Z on the average rate of participation (i.e. at the external margin) is obtained by differentiating P with respect to Z:

which depends on the sign of b. Since the second derivative is:

the marginal effect increases when the rate of participation is less than 0.5 (because z* is negative) and decreases otherwise.

The marginal effect of Z on y > 0 (i.e. at the internal margin is):

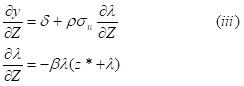
where l is calculated using z*. In equation (iii) it is assumed that Z is a component of X. Hence, d is the direct effect of Z on y, and the second term is the indirect effect through the external margin. Notice that even if the direct effect is zero (because Z is not a component of X), the variables that affect participation also affect y. 

The expected value of y at the internal margin (the conditional expectation) is:

where bars denote sample averages.  The unconditional expected value E(y) is the probability of participation multiplied by equation (iv), i.e. PE(y > 0). Therefore, the marginal effect of Z on the unconditional expected value of y is:

which may be calculated using equations (i), (iv) and (v).