The incidentally truncated regression method (ITR Heckman 1976) hypothesizes two populations. The first population does not participate in the outcome of interest hence the outcome is zero, and the second participates in which event the outcome is positive. Let y_i denote the outcome for individual i, which is zero if she belongs to the first population, and is positive if she belongs to the second. Positive outcomes are hypothesized to depend on a set of covariates X_i with regression residual denoted by u_i. A latent variable y_i* is hypothesized to depend on covariates Z_i and a random variable e_i, which measures individual i’s unobserved susceptibility to participate. If y_i* is insufficiently small (negative) individual i belongs to the first population in which case y_i is negative, and is positive otherwise.

ITR assumes that u and e are bivariate normal random variables with correlation denoted by r, which is a parameter to be estimated. If r is positive, individuals with a greater susceptibility to participate (e) have larger positive outcomes for y if they participate. For example, individuals with a greater susceptibility to employment, work more if they are employed.  If r is negative, individuals more susceptible to participate have smaller outcomes if they participate. If r is zero, the two populations are independent, in which case it would have been appropriate to estimate the relation between y and X using data for the second population on its own.

The probability of participation for individual i equals F_i = F(z_i) where z_i = a + βZ_i has a standard normal distribution. Let P denote the rate of participation in the data, and z* = F^-1(P) denote the value of z, which is implied by the average rate of participation in the data.  The marginal effect of Z on the average rate of participation (i.e. at the external margin) is obtained by differentiating P with respect to Z:

which depends on the sign of b. Since the second derivative is:

the marginal effect increases when the rate of participation is less than 0.5 (because z* is negative) and decreases otherwise.

The marginal effect of Z on y > 0 (i.e. at the internal margin is):

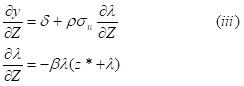
where l is calculated using z*. In equation (iii) it is assumed that Z is a component of X. Hence, d is the direct effect of Z on y, and the second term is the indirect effect through the external margin. Notice that even if the direct effect is zero (because Z is not a component of X), the variables that affect participation also affect y. 

The expected value of y at the internal margin (the conditional expectation) is:

where bars denote sample averages.  The unconditional expected value E(y) is the probability of participation multiplied by equation (iv), i.e. PE(y > 0). Therefore, the marginal effect of Z on the unconditional expected value of y is:

which may be calculated using equations (i), (iv) and (v).