Citation:
| dou2020range.pdf | 1.2 MB |
Abstract:
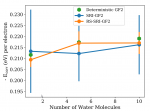
We develop a range-separated stochastic resolution of identity (RS-SRI) approach for the four-index electron repulsion integrals, where the larger terms (above a predefined threshold) are treated using a deterministic RI and the remaining terms are treated using a SRI. The approach is implemented within a second-order Green’s function formalism with an improved O(N3) scaling with the size of the basis set, N. Moreover, the RS approach greatly reduces the statistical error compared to the full stochastic version [T. Y. Takeshita et al., J. Chem. Phys. 151, 044114 (2019)], resulting in computational speedups of ground and excited state energies of nearly two orders of magnitude, as demonstrated for hydrogen dimer chains and water clusters.